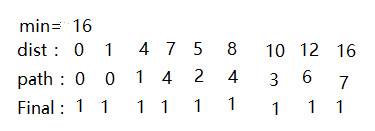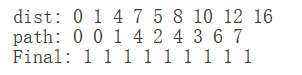Dijkstra算法实现最短路径

最短路径的实现——Dijkstra算法

Dijkstra算法实现最短路径

概述

现在给出一个无向网G现在让你从0点开始求出到每个点的最短路径如下图：
在这里插入图片描述

首先我们也不需要去考虑什么算法怎么去实现啊，怎么写代码之类的问题，现在就考虑一下如果让我们自己去选择最短路径，选择出来一个路径会是什么样的呢？

以人正常的思维就是从起始点依次开始找下一个点，并保证当前的选择是距离最短的步骤如下

以vo为起始点，有v0-v2,v0-v1两条路线可以选择，距离短的明显就是1，即v0-v1的最短路径为1，所以在走之后的路径时就以v1探索，找接下来找那个点路径最短。

从v1开始有v0-v1-v2，v0-v1-v3，v0-v1-v4，通过观察还是从v1到v2的路径更短，选择v2 ，此时v0-v2的最短路径就选出来了。

从v2起始有两种选择v0-v1-v2-v4，v0-v1-v2-v5，观察还是由v2-v4的路径更短，选择v4 此时从v0-v4的最短路径就找到了。
以此类推，就可以找到最短的路径

通过刚刚叙述的思想得到最短路径如下图：
在这里插入图片描述

Dijkstra算法思想

Dijkstra的思想就是刚刚我们说的那种方法，去找到最短的路径，主要通过贪心的思想实现，声明一个dist数组来保存起始点到其他点的距离，用集合T来保存已经求得最短路径的点，现在在dist数组中找到最小值的点，并将其纳入T中，下次探索就是从刚刚找的点开始再次寻找路径最小的点，直到所有的顶点纳入T中，完成了所有找最短路径的过程。

用一个简单的图为例：

在这里插入图片描述

以源点i为起始到顶点j为例,简单说i到k的有更短的距离i-j，所以将j点纳入T中，由j到k，再将k纳入T中，就找的了最短的路径，其实这就是Dijkstra的思想大概意思，说白了就是起始点到目标点有更近的路，换个路线，将换路线经过的点保存，图复杂的话就多次执行而已。

Dijkstra算法过程

设置关键数组

应该对Dijkstra算法那个思想有点明白的话，接下来就看看如果用代码实现的话，应该怎么做呢？

实现Dijkstra算法要设置三个关键的数组dist，path，final:

dist表示起始点到每一个顶点的值，通过不断修正dist数组的值找到最短路径完成最短路径的查找后，dist数组就表示最短路径的值即v点到下标点的值假如v = 0, v[6] = 10, 0到6 的最短路径为10。

path数组用来保存前驱 , 类似于Prim中closevertex数组，如果path[2] = 1 说明2之前的顶点为 1,
完成最短路径的查找后 ,构成最短路径的每个点都有前驱，所以最终用来查看最短路径。

Final数组用来判断是否已经找到最短路径比如Finalp[2] = 1，说明从顶点0到顶点2已经找到了最短路径，表示该点就纳入了T中了，不需要进行判断。

具体图解过程

可能还是不清楚Dijkstra算法每步时如何实现的，接下来以刚刚的图为例通过这三个数组以及图示来说明过程(起点以v0为例，图中去掉了v)：

通过邻接矩阵表示：
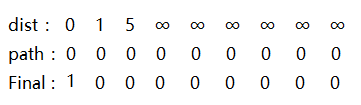
在这里插入图片描述

三个数组初始化为：
在这里插入图片描述
1.第一次选择路径最小值为1 如图：

对应数组如下：

声明：min选择最短路径的值，k代表下次开始选择的路径，如果k=1，代表下次从1开始探索路径，可以通过邻接矩阵查看以k为起始位置的那一行，去一一比较。

在这里插入图片描述

解释：此时的选择的最小值为1 将最小值1对应的Final数组标记为1，说明找到v0到v1的最短路径，接下来以顶点v1为最小值继续修正最短路径，v1可到达v3，v4，v2.通过dist数组暂时存储他们为最短路径。

2.第二次选择路径如图：
在这里插入图片描述
对应数组如下：

此时的选择的最小值为4 将最小4对应1的Final数组标记为1 ，说明找到v0到v2的最短路径，接下来以顶点v2为最小值继续修正最短路径，v2可到达v4，v5。通过dist数组暂时存储他们为最短路径。

3.第三次选择路径如图：
在这里插入图片描述
对应数组如下：

此时的选择的最小值为5 将最小为5对应的Final数组标记为1，说明找到v0到v4的最短路径，接下来以顶点v4为最小值继续修正，v4可到达v3，v5，v6，v7。通过dist数组暂时存储他们为最短路径。

4.第4次选择路径如图：
在这里插入图片描述
对应数组如下：

此时的选择的最小值为7 将最小7对应的Final数组标记为1，说明找到v0到v3的最短路径，接下来以顶点v3为最小值继续修正，v3可到达v6.通过dist数组暂时存储他们为最短路径。

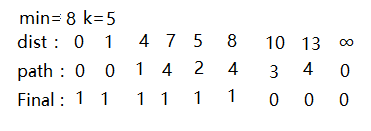
5.第5次选择路径如图：
在这里插入图片描述
对应数组如下：

此时的选择的最小值为8，将最小8处对应的Final数组标记为1，而此时v3无法到达v5，这时意思就是标记已经走过了改路径。

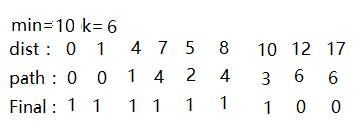
6.第6次选择路径如图：
在这里插入图片描述
对应数组如下：

此时的选择的最小值为10 将最小10处对应的Final数组标记为1，，说明找到v0到v6的最短路径，接下来以顶点v6为最小值继续修正最短路径，v6可到达v7，v8。通过dist数组暂时存储他们为最短路径。

7.第7次选择路径如图：
在这里插入图片描述
对应数组如下：

此时的选择的最小值为12 将最小12处对应的Final数组标记为1，，说明找到v0到v7的最短路径，接下来以顶点v7为最小值继续修正最短路径，v7可到达v8。通过dist数组暂时存储他们为最短路径。

8.第八次路径选择如图：在这里插入图片描述
对应的数组为：

通过以上的过程我们就构建了最短路径，dist数组最终就表示了v0到各个顶点的权值，path数组表示了构成最短路径的点。

Dijkstra算法实现

void Dijkstra(Graph G, int v){
   int min, k, dist[MAX_VEX], path[MAX_VEX], Final[MAX_VEX];
   for(int i = 0; i < G.numvex; i++){
           dist[i] = G.arc[v][i];     //数组初始化dist数组含义为；从顶点v到其他任一点的距离
           path[i] = 0;               //初始化路径数组
           Final[i] = 0;              // 初始化标记数组
   }
   dist[v] = 0;                       // v到自身的距离为 0
   Final[v] = 1;                      // 自身的点不需要判断
   for(int i = 0; i < G.numvex; i++){ // 主循环找到v到顶点i的最小值
       min = INF;
       for(int j = 0; j < G.numvex; j++){
           if(!Final[j] && min > dist[j]){
               min = dist[j];
               k = j;
           }
       }
       cout<< k<< " ";
       Final[k] = 1;                    // 将找到距离最小的顶点标记为1
       for(int j = 0; j < G.numvex; j++){
           /*将之前求得到某点最短路径的值与从某点到j的距离之和  与 v 到 j 的路径大小比较
           如果前者小，设置为v到j的最短路径*/
           if(!Final[j] &&(min + G.arc[k][j] < dist[j])){
               dist[j] = min + G.arc[k][j];
               path[j] = k;				//保存前驱
           }
       }
   }
}

Dijkstra算法完整过程

#include <iostream>
#include <cstdio>
#define MAX_VEX 100
#define INF 65535

using namespace std;
struct Graph{
    char vexs[MAX_VEX];
    int arc[MAX_VEX][MAX_VEX];
    int numvex,numarc;
};
void CreateGraph(Graph &G){
    int vi, vj, w;
    cout << "please enter the number of vertexes and arcs : \n";
    cin >> G.numvex >> G.numarc;
    for(int i = 0; i < G.numvex; i++){
        printf("Please enter the NO.%d name of vex : ",i+1);
        cin >> G.vexs[i];
    }

    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex ;j++){
            G.arc[i][j] = INF;
        }
    }
    cout << endl;
    for(int i = 0; i < G.numarc; i++){
        cout<< "Enter the subscripts and weights from vertex vi to vertex vj : ";
        cin >> vi >> vj >> w;
        G.arc[vi][vj] = w;
        G.arc[vj][vi] = w;
    }
}
void DispalyGraph(Graph G){
    for(int i = 0; i < G.numvex; i++)
        printf("%c ", G.vexs[i]);
        cout << endl;
    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex; j++){
            if(G.arc[i][j] == INF) printf("%6s", "∞");
            else printf("%6d", G.arc[i][j]);
        }
        cout << endl;
    }
}
void Dijkstra(Graph G, int v){
    int min, k, dist[MAX_VEX], path[MAX_VEX], Final[MAX_VEX];
    for(int i = 0; i < G.numvex; i++){
            dist[i] = G.arc[v][i];     
            path[i] = 0;              
            Final[i] = 0;              
    }
    dist[v] = 0;                      
    Final[v] = 1;                     
    for(int i = 0; i < G.numvex; i++){ 
        min = INF;
        for(int j = 0; j < G.numvex; j++){
            if(!Final[j] && min > dist[j]){
                min = dist[j];
                k = j;
            }
        }
        cout<< k<< " ";
        Final[k] = 1;                  
        for(int j = 0; j < G.numvex; j++){
            if(!Final[j] &&(min + G.arc[k][j] < dist[j])){
                dist[j] = min + G.arc[k][j];
                path[j] = k;
            }
        }
    }
    // 在此依次输出dist path final 数组的信息
    cout << endl;
    cout << "dist: ";
    for(int i = 0; i < G.numvex; i++)  cout << dist[i] << " ";
    cout << endl;
    cout << "path: ";
    for(int i = 0; i < G.numvex; i++) cout << path[i] << " ";
    cout << endl;
    cout << "Final: ";
    for(int i = 0; i < G.numvex; i++) cout << Final[i] << " ";
   
}
int main(){
    Graph G;
    CreateGraph(G);
    DispalyGraph(G);
    Dijkstra(G,0);
    return 0;
}
/*
0 1 1
0 2 5
1 3 7
1 4 5
4 2 1
2 3 7
3 6 3
6 4 6
4 7 9
7 5 5
6 8 7
7 8 4
1 2 3
3 4 2
4 5 3
6 7 2
*/

运行结果

运行结果如下：
在这里插入图片描述

分析

分析一下这个算法的运行时间，第一个for循环的时间复杂度为O() 第二个for总共进行n-1次执行时间为O()，总的时间复杂度为O( )。