线索二叉树的建立

线索二叉树

线索二叉树概念

二叉树通过二叉链表作为存储结构时，只能得到当前结点的左右孩子信息，而无法得到结点在任一序列的前驱和后继，如果想要保存遍历中的信息,需要在每个结点上添加两个指针域，分别指向当前结点的前驱和后继，指向线性序列中的前驱和后继的指针，称为线索，
并且增加两个标志域 如下图

设置规定如下：

ltag=0 表示lchild 指向左孩子
latg=1 表示lchild 指向前驱
rtag=0 表示rchild 指向右孩子
rtag=1 表示rchild 指向后继

按照上述的原则 在二叉树中添加线索的过程叫二叉树的线索化

线索二叉树图解

假设给定下图的二叉树

这时可以根据中序遍历的结果来对二叉树线索化 ，中序遍历的结果为：DGBAECF
如下图
实线指的是二叉树所指向的结点
虚线指的是线索

解释一下 建立线索的过程

  1. A节点左右孩子存在，ltag=0，lchild指向左孩子B，rtag=0 ，rchild指向右孩子C。
  1. B节点左孩子存在 ltag=0，lchild指向左孩子D，右孩子不存在 rtag=1，根据中序遍历的结果B的后继为A，rchild 指向后继结点A。
  2. C节点左右孩子存在，ltag=0，lchild指向左孩子E， rtag=0 rchild指向右孩子F。
  3. D节点无左孩子，ltag=1，根据中序遍历的结果D之前没有元素 lchild指向前驱根节点，rtag=0 ，rchild 指向右孩子G。
  4. E节点不存在左右孩子 ltag=1 ，根据中序遍历E的前驱为A，lchild 指向前驱A rtag=1 根据中序遍历E的后继为C，rchild 指向后继C。
  5. F节点不存在左右孩子 ltag=1，根据中序遍历F的前驱为c，lchild指向前驱C， rtag=1，根据中序遍历F的后继为根 rchild 指向后继根
  6. G节点不存在左右孩子，ltag=1，根据中序遍历G的前驱为D，lchild指向前驱D，rtag=1，根据中序遍历G的后继为B ，rchild 指向后继B

同理可以得到前序遍历线索二叉树为：

解释一下过程：

  1. 节点A存在左右孩子，lchild指向B，rtag=0 ，rchild指向C。
  2. 节点B有左孩子，ltag=0，lchild指向D，无右孩子 rtag=1，由前序遍历得，rchild指向后继D。
  3. 节点C存在左右孩子，ltag=0 lchild指向E，rtag=0 ，rchild指向F。
  4. 节点D无左孩子，ltag=1，由前序遍历得，lchild指向前驱B，有有孩子 rtag=0，rchild指向后继G。
  5. 节点E无左右孩子，ltag=1，由前序遍历得，lchild指向前驱C，rtag=1，由前序遍历得，lchild指向后继F。
  6. 节点F无左右孩子，ltag=1，由前序遍历得，lchild指向前驱E，rtag=1，由前序遍历得，lchild指向后继根。
  7. 节点G无左右孩子，ltag=1，由前序遍历得，lchild指向前驱D，rtag=1，由前序遍历得，lchild指向后继C。

如图后序的线索二叉树为：

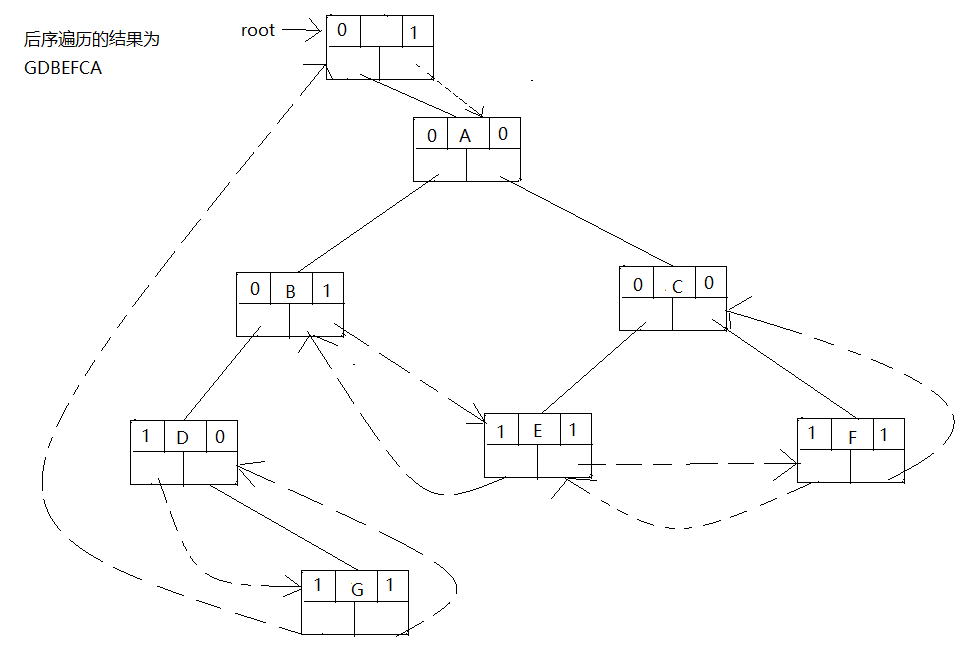
解释一下过程：

  1. 节点A存在左右孩子，lchild指向B，rtag=0 ，rchild指向C。
  2. 节点B有左孩子，ltag=0，lchild指向D，无右孩子 rtag=1，由后序遍历得，rchild指向后继E。
  3. 节点C存在左右孩子，ltag=0 lchild指向E，rtag=0 ，rchild指向F。
  4. 节点D无左孩子，ltag=1，由后序遍历得，lchild指向前驱G，有右孩子 rtag=0，rchild指向后继G。
  5. 节点E无左右孩子，ltag=1，由后序遍历得，lchild指向前驱B，rtag=1，由后序遍历得，lchild指向后继F。
  6. 节点F无左右孩子，ltag=1，由后序遍历得，lchild指向前驱E，rtag=1，由后序遍历得，lchild指向后继C。
  7. 节点G无左右孩子，ltag=1，由后序遍历得，lchild指向前驱根，rtag=1，由后序遍历得，lchild指向后继D。

线索二叉树代码实现

大致知道了线索是怎么回事，看看以中序为例代码的实现方式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <stdio.h>
#include <stdlib.h>
typedef struct BiThtree{
    char data;
    int rtag,ltag;
    struct BiThtree *Lchild,*Rchild;
}Bitree,   *BiTHree;

BiTHree pre;               // 设置临时结点，保存之前访问的节点

void InitTree(BiTHree *T){ //二叉树的初始化
    char  c;
    scanf("%c",&c);
    if(c==' '){
        *T=NULL;
    }else{
        *T=(Bitree*)malloc(sizeof(Bitree));
        (*T)->data=c;
        (*T)->ltag=0;
        (*T)->rtag=0;
        InitTree(&(*T)->Lchild);
        InitTree(&(*T)->Rchild);
    }
}
//中序线索化二叉树
void Inthreading(BiTHree T){
    if(T){
        Inthreading(T->Lchild);
        if(!T->Lchild){    //左孩子不存在时 
            T->ltag=1;
            T->Lchild=pre; //Lchild指向刚刚访问的节点
        }
        if(!pre->Rchild){ //右孩子不存时
            pre->rtag=1;
            pre->Rchild=T; //Rchild指向上一个访问的节点 
        }
        pre=T;  访问结束后将上一个节点赋值给pre
        Inthreading(T->Rchild);
    }
}
/*设置根节点，二叉树线索化是动态的过程，中序遍历时第一个元素的前驱指向根节点，末尾元素的后继也指向根。
*/
void Inorderthreading(BiTHree *root, BiTHree T)
{
     *root =(Bitree*)malloc(sizeof(BiTHree));
     (*root)->ltag=0;
     (*root)->rtag=1;
     if(!T){
         (*root)->Lchild=*root;
     }else{
        (*root)->Lchild=T;
        pre=*root;
        Inthreading(T);          //线索化完成pre为最后一个节点
        pre->Rchild=*root;       //末尾元素指向根
        pre->rtag=1;             //标记为1
        (*root)->Rchild=pre;     //根的右孩子指向末尾元素
     }
}
void visit(char c)                  
{
    printf("%c",c);
}
void InOrderTraverse( BiTHree T )    //以迭代的方式遍历二叉树
{
    BiTHree p;
	p = T->Lchild;
	while( p != T )
	{
		while( p->ltag ==0)
		{
			p = p->Lchild;
		}
		visit(p->data);
		while( p->rtag == 1 && p->Rchild != T )
		{
			p = p->Rchild;
			visit(p->data);
		}
		p = p->Rchild;
	}
}
int main()
{

    BiTHree T =NULL,root=NULL;
    InitTree(&T);
    Inorderthreading(&root,T);
    printf("中序遍历为：\n");
    InOrderTraverse(root );
    return 0;
}