Kruskal算法构建最小生成树
|Word Count:1.2k|Reading Time:5mins|Post Views:
最小生成树的实现——Kruskal算法
Kruskal算法的思想
Kruskal算法是一种通过按权值依次递增的次序来选择适当的边来构建最小生成树的,在无向连通网G=(V,E)中,假设G的最小生成树为T=(V,{}),起始转态最小生成树有G中的全部顶点构成,并且没有任何一条边,之后按照边的权值有递增的顺序排列,依次查询G中的边集E,如果查询的边的两个顶点属于两个不同的连通分量,就将这条边纳入到T中去,并将两个连通分量连接为一个连通分量,如果查询的边的两个顶点属于一个连通分量就舍弃此边,避免造成回路。反复执行此过程,当T中的连通分量的个数为1时,这样我们也就找到了最小生成树。
Kruskal算法的图解过程
假设我们给定如下的图,通过Kruskal算法的思想应该怎么构成最小生成树呢?
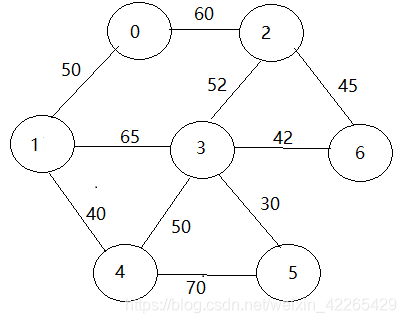
刚刚说的概念可能还是不太理解的话,那么简单一句话总结,按照权值依次递增 的顺序选取边,如果构成回路,就将此边舍去。接下来就看一下图解过程:
- 第一次构建:
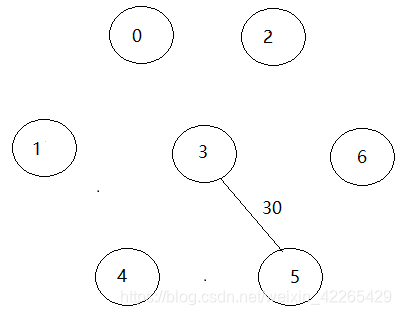
- 第二次构建:
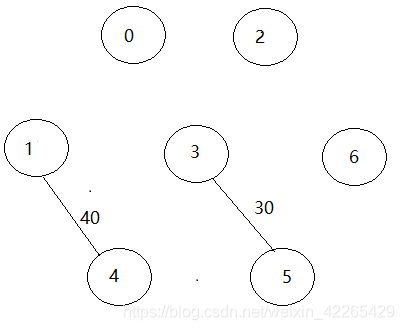
- 第三次构建:
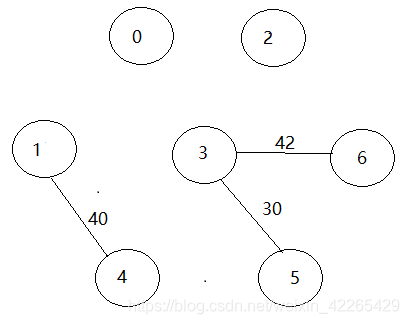
- 第四次构建:
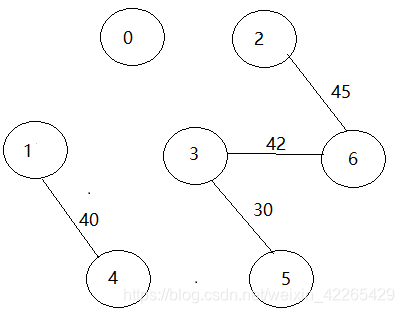
5.第五次构建:
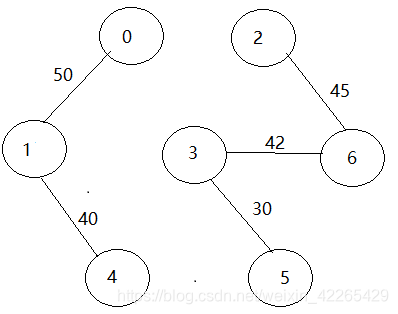
6.第六次构建:
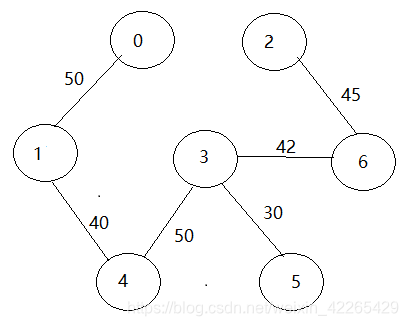
实现Kruskal算法添加的关键结构
通过刚刚的构建的邻接矩阵中的边的信息通过结构体数组保存
1
2
3
4
5
| struct Edge{
int beg;
int des;
int wei;
};
|
Kruskal算法的实现过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| int Find(int parent [],int f){
while(parent[f] > 0) f = parent[f];
return f;
}
void Kruskal(Graph G){
Edge e[MAX_VEX];
int parent[MAX_VEX], k = 0, m ,n;
for(int i = 0; i < G.numvex; i++){
for(int j = 0; j < G.numvex; j++){
if(G.arc[i][j] != 0 && G.arc[i][j] != INFINITY){
e[k].beg = i; e[k].des = j; e[k].wei = G.arc[i][j];
k++;
}
}
}
sort(e,e+k,cmp);
for(int i = 0; i < k; i++) parent[i] = 0;
cout << "Kruskal:\n";
for(int i = 0; i < k; i++){
m = Find(parent,e[i].beg);
n = Find(parent,e[i].des);
if(m != n){
parent[m] = n;
printf("%d %d %d \n", e[i].beg, e[i].des, e[i].wei);
}
}
}
|
完整的实现过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
| #include <iostream>
#include <algorithm>
#include <cstdio>
#define MAX_VEX 100
#define INF 65535
using namespace std;
struct Graph{
char vexs[MAX_VEX];
int arc[MAX_VEX][MAX_VEX];
int numvex,numarc;
};
struct Edge{
int beg,des,wei;
};
void CreateGraph(Graph &G){
int vi, vj, w;
cout << "please enter the number of vertexes and arcs : \n";
cin >> G.numvex >> G.numarc;
for(int i = 0; i < G.numvex; i++){
printf("please input the NO.%d name of vex :",i+1);
cin >> G.vexs[i];
}
for(int i = 0; i < G.numvex; i++){
for(int j = 0; j < G.numvex ;j++){
G.arc[i][j] = INF;
}
}
cout << endl;
for(int i = 0; i < G.numarc; i++){
cout << "Enter the subscripts and weights from vertex vi to vertex vj : ";
cin >> vi >> vj >> w;
G.arc[vi][vj] = w;
G.arc[vj][vi] = w;
}
}
void DispalyGraph(Graph G){
for(int i = 0; i < G.numvex; i++) cout << G.vexs[i];
cout << endl;
for(int i = 0; i < G.numvex; i++){
for(int j = 0; j < G.numvex; j++){
if(G.arc[i][j] == INF) printf("%6s", "¡Þ");
else printf("%6d", G.arc[i][j]);
}
cout << endl;
}
}
bool cmp(Edge a ,Edge b){
return a.wei < b.wei;
}
int Find(int parent [],int f){
while(parent[f] > 0) f = parent[f];
return f;
}
void Kruskal(Graph G){
Edge e[MAX_VEX];
int parent[MAX_VEX], k = 0, m ,n;
for(int i = 0; i < G.numvex; i++){
for(int j = 0; j < G.numvex; j++){
if(G.arc[i][j] != 0 && G.arc[i][j] != INFINITY){
e[k].beg = i; e[k].des = j; e[k].wei = G.arc[i][j];
k++;
}
}
}
sort(e,e+k,cmp);
for(int i = 0; i < k; i++) parent[i] = 0;
cout << "Kruskal:\n";
for(int i = 0; i < k; i++){
m = Find(parent,e[i].beg);
n = Find(parent,e[i].des);
if(m != n){
parent[m] = n;
printf("%d %d %d \n", e[i].beg, e[i].des, e[i].wei);
}
}
}
int main(){
Graph G;
CreateGraph(G);
DispalyGraph(G);
Kruskal(G);
return 0;
}
|
实现结果
实现结果如下图:

分析
Kruskal算法是根据边来构建最小生成树的,所以与顶点无关,用于在稀疏图中更合适,时间复杂度为









