串的模式匹配算法(BF KMP及优化)

朴素的模式匹配算法

  • 串的模式匹配是查询主串中是否含有与之匹配的字串，有则返回从主串开始匹配位置后的第一次出现子串的位置，否则返回。

以下图为例：
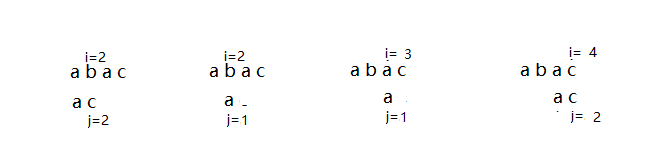
在这里插入图片描述

主串s中存在相同值的子串t 返回在s中pos后第一次出现的位置 否则 返回 0

代码如下 ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef char * String ;
int getindex(String s ,String t,int pos){
    int i=pos;
    int j=0;
    while(i<strlen(s)&&j<strlen(t)){
        if(s[i]==t[j]){
            i++;
            j++;
        }else{
            j=0;
            i=i-(j-1);
        }
    }
    if(j>=strlen(t)){
        return i-strlen(t)+1;
    }else {
        return 0;
    }
}
int main()
{
    char s[255]="abac";
    char t[255]="ac";
    int i=getindex(s,t,0);
    printf("%d",i);
    if(i){
        printf("匹配字符串的起始位置为：%d",i);
    }else{
        printf("匹配失败\n");
    }
    return 0;
}

上述代码是通过从字符串的第0个位置开始计算的，并不是按照书上通过s[0] t[0] 存储字符串的长度 (那种方式主要是自己不会) 而平时串的起始位置时从一开始 ，即返回位置时应当加1。

如下图所示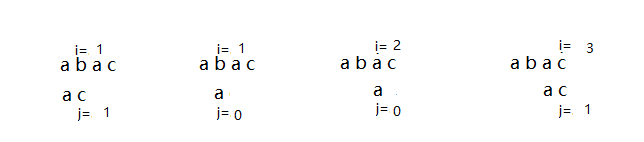：在这里插入图片描述

KMP算法

KMP算法是对朴素的模式匹配算法的一种改进，在BF算法中是通过回溯模式串的方式与主串的字符一一比较是否匹配，而KMP算法不需要回溯模式串提高了效率。

注意便于解释与计算 主串s和模式串t都从第一个元素开始比较，即忽略掉s[0]和t[0]

  • 考虑下面几种情况：

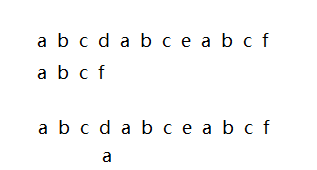
在这里插入图片描述

由上图看并没有回溯模式串,而是将主串失配的位置与模式串的第一个元素比较,主串s中的s[1] s[2] s[3] 分别与模式串中的t[1] t[2] t[3]
的元素匹配，明显地，模式串中的t[1] 与 t[2] t[3] 都不匹配，所以t[1] 与主串的中的元素s[2] s[3] 必然不相等 ，所以下次匹配的位置就应当从主串的s[4]开始匹配，通过这样的思想赋给模式串的j一个不用回溯的位置数字，减少不必要的重复。

还存在另一种情况 在这种情况下应该怎样继续进行匹配呢？
在这里插入图片描述

如果这种情况下失配的话以正常思维来看的话 应当从t[3]的位置开始继续匹配字符串如在这里插入图片描述

  • 原因从图中看比较明显，模式串中第六个元素失配，所以主串第一个到第五个元素是和模式串中的元素匹配的， 而模式串中的第一个，第二个元素 分别于其第四个，第五个元素一致，即t[1]=t[4],t[2]=t[5],所以模式串中的第一个，第二个元素于主串中的第四个 第五个元素一致 即t[1]=s[4] t[2]=s[5],下次开始从模式串中的t[3]开始，下次模式串匹配的起始位置就为3。
  • 通过这样的方法，假设模式串中每个元素都可能失配，类似一个像前边提到的例子一样，赋给每个失配的元素下次起始匹配的位置，即每个模式串中失配时，都有一个对应的数字来表示下次起始匹配得位置，我们将这些数字通过一个数组来表示，也把这样的数组称为next数组。

  • 参考教材得到如下规律：
    假设主串为s _{1} s _{2} …s _{n} 模式串为p _{1} p _{2} …p _{n} 主串中第i个字符与模式串中的第j个字符失配时，主串中的第i个字符应该与模式串中的那个字符比较 ？
    假设与模式串中的第k个字符继续比较得到此关系式（重点从模式串中k位置继续比较）得到一下关系：

    p _{1} p _{2} …p _{k-1} =s _{i-k+1} s _{i-k+2} …s _{i-1}

    还可以得：
    p _{j-k+1} p _{j-k+2} …p _{j-1} =s _{i-k+1} s _{i-k+2} …s _{i-1}

    由上述两个式子得：
    p _{j-k+1} p _{j-k+2} …p _{j-1} = p _{1} p _{2} …p _{k-1}

    公式可能会看的比较迷惑，公式的大致意思如下图：
    在这里插入图片描述

  • 在本例当中假设继续比较的位置为3（3为公式中的k），那么相等的就是两个红圈圈的元素 通过上述的公式理解 ,即可得t[1]=t[4],t[2]=t[5], 这样下次模式串中下次匹配的位置 就为3 。
  • 通过公式的推导可知，next数组的求解的过程时和主串中的元素无关的。
  • next 数组的含义
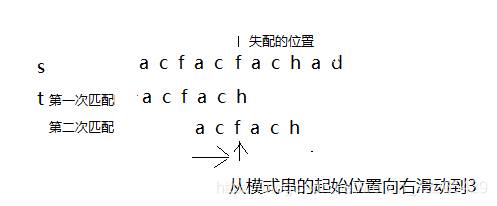
    在这里插入图片描述

由图可知，第二次从模式串起始位置右滑动到模式串的第三个元素，即模式串中失配的t[6]位置对应的next数组next[6]=3, 意思为如果在模式串t[6]的位置失配时，下次从模式串的起始位置向右滑动的距离为3.
同理，假设模式串中每个元素都有可能出现失配的情况，对每一个元素对应的next数组赋给的值就是失配后从模式串起始位置向右滑动的距离。

  • next数组的求解

那么给定模式串的话是怎么求得next数组中与其一一对应的值？通过观察是否有模式串是否存在一定的规律来直接求得next数组的值呢 ？在求next数组之前先了解一下模式串元素的特点 ——对称性（并不是数学中完全意义的对称）
如下图：
在这里插入图片描述

以刚刚的的情况为例，在模式串中失配的位置为模式串中的第六个元素，类似的可以看成前个五元素有对称性 前五个元素中可以看到红圈位置的元素是相等的（以f为中心的前两个和后两个从左到右的元素对称相等，这一点和数学上的对称不是一个意思，类似理解即可）把f之前的两个元素称为前缀，之后的元素称为后缀，通过观察得，前缀与后缀的元素相等的个数为2，而next数组的值就是前缀后缀元素相等的个数+1。

在对称的时候会出现重叠 情况如下图：
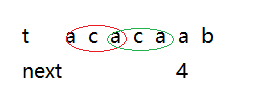
在这里插入图片描述

而重叠的情况下也是会算入到前缀后缀相等的计算过程中

还有特殊的情况，如下图：
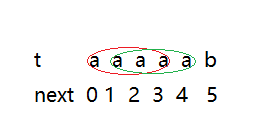
在这里插入图片描述

这种情况类似称为最大对称性，以t[5]为例，前缀和后缀相等元素的值为4 所以b元素对应得next数组得值为5

以下图为例求出所有模式串中所有next数组得值：

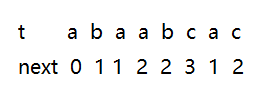
在这里插入图片描述

  • KMP的全过程
    了解了next的含义以及求解过程 以主串s=’‘acabaabaabcacaabc’'模式串t="abaabcac"为例解释KMP的全过程 ：

在这里插入图片描述
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef char * String ;
void getnext(String t ,int *next)
{
    int i=1;
    int j=0;
    next[1]=0;
    while(i<strlen(t)){
        if(j==0||t[i]==t[j]){
            i++;
            j++;
            next[i]=j;
        }
        else{
            j=next[j];
        }
    }
}
int getindex(String s ,String t,int pos){
    int i=pos;
    int j=1;
    int next[255];

    getnext(t,next);
    while(i<strlen(s)&&j<strlen(t)){
        if(j==0||s[i]==t[j]){
            i++;
            j++;
        }else{
            j=next[j];
        }
    }
    if(j>=strlen(t)){
        return i-strlen(t)+1;
    }else {
        return 0;
    }
}
int main()
{
    String s=" acabaabaabcacaabc";
    String t=" abaabcac";
    int i =getindex(s,t,1);
    printf("%d",i);
    return 0;
}

执行结果如下
在这里插入图片描述

  • 优化KMP
    以上已经大致介绍了KMP算法，但是还存在一些不足之处，有待改进， 我们考虑这样的情况 如下图所示

在这里插入图片描述

在这种情况下依然出现了多余比较的情况，对此我们可以进行修改：在next数组中存在下一个元素和之前的前缀元素相等的话就改为前缀元素next数组的值 使下一个元素next数组的值和前缀next数组的值相同， 改进后情况如下：

在这里插入图片描述
代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void getnext(String t ,int *next)
  {
      int i=1;
      int j=0;
      next[1]=0;
      while(i<strlen(t)){
          if(j==0||t[i]==t[j]){
              i++;
              j++;
              if(t[i]!=t[j]){
              
              next[i]=j;
              }else{
              next[i]=next[j];
              }
          }
          else{
              j=next[j];
          }
      }
  }

总结： 以上是自己对模式匹配算法的理解，应该还是有很多理解不对或疏漏的地方，希望能帮忙指正，我会及时修改